Master Method

The Master Method is used for solving the following types of recurrence

T (n) = a T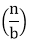+ f (n) with a≥1 and b≥1 be constant & f(n) be a function and 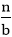can be interpreted as

Let T (n) is defined on non-negative integers by the recurrence.

 T (n) = a T+ f (n)

In the function to the analysis of a recursive algorithm, the constants and function take on the following significance:

• n is the size of the problem.
• a is the number of subproblems in the recursion.
• n/b is the size of each subproblem. (Here it is assumed that all subproblems are essentially the same size.)
• f (n) is the sum of the work done outside the recursive calls, which includes the sum of dividing the problem and the sum of combining the solutions to the subproblems.
• It is not possible always bound the function according to the requirement, so we make three cases which will tell us what kind of bound we can apply on the function.

Master Theorem:

It is possible to complete an asymptotic tight bound in these three cases:

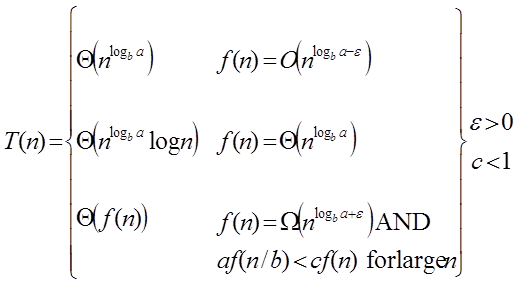
Case1: If f (n) = 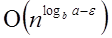 for some constant ε >0, then it follows that:

T (n) = Θ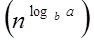 

Example:

T (n) = 8 T  apply master theorem on it.

Solution:

Compare T (n) = 8 T  with 
 T (n) = a T 
 a = 8, b=2, f (n) = 1000 n2, logba = log28 = 3
 Put all the values in: f (n) = 
     1000 n2 = O (n3-ε ) 
     If we choose ε=1, we get: 1000 n2 = O (n3-1) = O (n2)

Since this equation holds, the first case of the master theorem applies to the given recurrence relation, thus resulting in the conclusion:

T (n) = Θ 
   Therefore: T (n) = Θ (n3) 

Case 2: If it is true, for some constant k ≥ 0 that:

F (n) = Θ  then it follows that: T (n) = Θ 

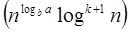
Example:

T (n) = 2 , solve the recurrence by using the master method.
As compare the given problem with T (n) = a T a = 2, b=2, k=0, f (n) = 10n, logba = log22 =1 
Put all the values in f (n) =Θ , we will get 
	10n = Θ (n1) = Θ (n) which is true.
Therefore: T (n) = Θ 
      = Θ (n log n)

Case 3: If it is true f(n) = Ω 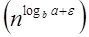 for some constant ε >0 and it also true that: a f  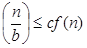for some constant c<1 for large value of n ,then :

1. T (n) = Θ((f (n))   

Example: Solve the recurrence relation:

T (n) = 2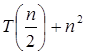 

Solution:

Compare the given problem with T (n) = a T 
a= 2, b =2, f (n) = n2, logba = log22 =1 
Put all the values in f (n) = Ω  ..... (Eq. 1)
If we insert all the value in (Eq.1), we will get 
  n2 = Ω(n1+ε) put ε =1, then the equality will hold.
  n2 = Ω(n1+1) = Ω(n2)
Now we will also check the second condition:
  2 
If we will choose c =1/2, it is true:
    ∀ n ≥1 
So it follows: T (n) = Θ ((f (n))
    T (n) = Θ(n2)

---