Recursion Method

 

Recursion Tree Method

1. Recursion Tree Method is a pictorial representation of an iteration method which is in the form of a tree where at each level nodes are expanded.

2. In general, we consider the second term in recurrence as root.

3. It is useful when the divide & Conquer algorithm is used.

4. It is sometimes difficult to come up with a good guess. In Recursion tree, each root and child represents the cost of a single subproblem.

5. We sum the costs within each of the levels of the tree to obtain a set of pre-level costs and then sum all pre-level costs to determine the total cost of all levels of the recursion.

6. A Recursion Tree is best used to generate a good guess, which can be verified by the Substitution Method.

Example 1

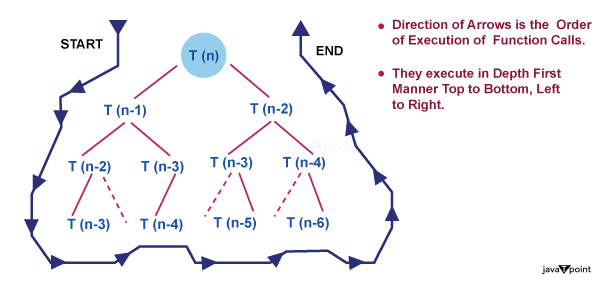
 Consider T (n) = 2TDAA Recurrence Relation + n2

We have to obtain the asymptotic bound using recursion tree method.

Solution: The Recursion tree for the above recurrence is

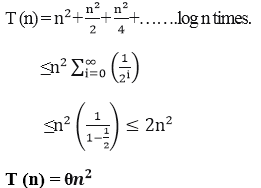
DAA Recursion Tree Method
DAA Recursion Tree Method

Example 2: Consider the following recurrence

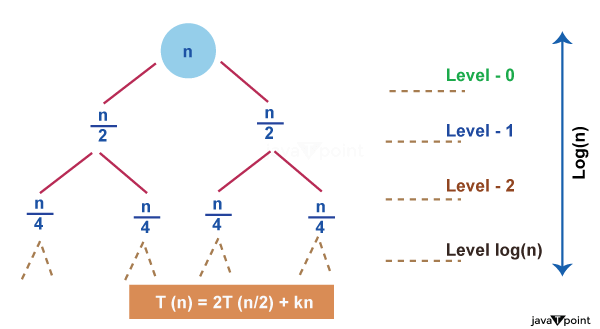
 T (n) = 4TDAA Recurrence Relation +n

Obtain the asymptotic bound using recursion tree method.

Solution: The recursion trees for the above recurrence

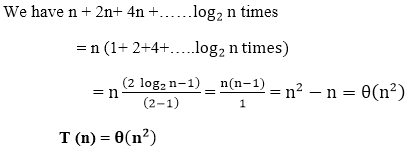
DAA Recursion Tree Method
DAA Recursion Tree Method

Example 3: Consider the following recurrence

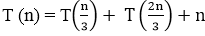
DAA Recursion Tree Method

Obtain the asymptotic bound using recursion tree method.

Solution: The given Recurrence has the following recursion tree

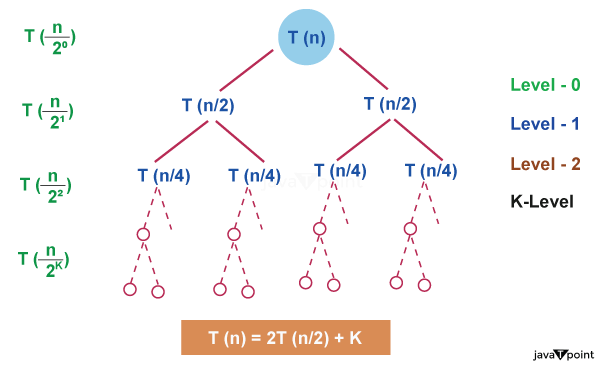
DAA Recursion Tree Method

When we add the values across the levels of the recursion trees, we get a value of n for every level. The longest path from the root to leaf is

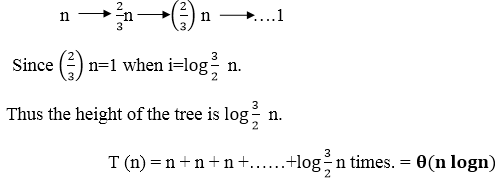
DAA Recursion Tree Method

Comments

Post a Comment

Popular posts from this blog

Recurrence Relation

Image
  Recurrence Relation A recurrence is an equation or inequality that describes a function in terms of its values on smaller inputs. To solve a Recurrence Relation means to obtain a function defined on the natural numbers that satisfy the recurrence. For Example , the Worst Case Running Time T(n) of the MERGE SORT Procedures is described by the recurrence. T (n) = θ (1) if n=1 2T + θ (n) if n>1 There are four methods for solving Recurrence: Substitution Method Iteration Method Recursion Tree Method Master Method 1. Substitution Method: The Substitution Method Consists of two main steps: Guess the Solution. Use the mathematical induction to find the boundary condition and shows that the guess is correct. For Example1  Solve the equation by Substitution Method. T (n) = T + n We have to show that it is asymptotically bound by O (log n). Solution: For T (n) = O (log n) We have to show that for some constant c T (n) ≤c logn.   Put this in given Recurrence Equation. T (n) ≤c log + 1
Read more

Substitution Method

Image
The Substitution Method Consists of two main steps: Guess the Solution. Use the mathematical induction to find the boundary condition and shows that the guess is correct. For Example1  Solve the equation by Substitution Method. T (n) = T + n We have to show that it is asymptotically bound by O (log n). Solution: For T (n) = O (log n) We have to show that for some constant c T (n) ≤c logn.   Put this in given Recurrence Equation. T (n) ≤c log + 1 ≤c log + 1 = c logn-clog 2 2+1 ≤c logn for c≥1 Thus T (n) =O logn . Example2  Consider the Recurrence T (n) = 2T + n n>1 Find an Asymptotic bound on T. Solution: We guess the solution is O (n (logn)).Thus for constant 'c'. T (n) ≤c n logn Put this in given Recurrence Equation. Now, T (n) ≤2c log +n ≤cnlogn-cnlog2+n =cn logn-n (clog2-1) ≤cn logn for (c≥1) Thus T (n) = O (n logn) . 2. Iteration Methods It means to expand the recurrence and express it as a summation of terms of n and initial condition. Exa
Read more